阿部技術士・労働安全コンサルタント事務所は、ものづくりの現場における労働安全の構築と品質の作り込みをサポートします。
TEL. 088-694-3482
〒771-1330 徳島県板野郡上板町西分字橋北１６番地２
技術情報メモ66Technical information
66)設計の勘どころ（力学の問題／ダランベールの原理）
力学の問題を解くためには物体に作用している力とその性質を知らなければなりません。そのためには、考えている座標系がどのようなものなのかをはっきりと認識しなければなりません。ここでは、慣性系と非慣性系の違いについて、加速している電車のつり革の動きで考えます。
図1は慣性系を説明したものです。
車外から電車を見ると、電車は右向きに加速しているように見えます。
●この場合、そのまま運動方程式を立てます。
図2は非慣性系を説明したものです。
車内から外を見ると、電車が加速しているので、静止したままの外の景色は電車の進行方向とは逆の向きに加速しているように見えます。
●この場合、見かけの力（慣性力）を加えて運動方程式を立てます。
慣性系において，力 Fが働いたとき質量 m の質点の加速度がa であるとすれば、質点の運動はニュートンの運動方程式 F＝ma によって決定されます。
この式の右辺を移項してF＋(−ma)＝0 と書直せば、非慣性系では、質点は力 F と 力（−ma）により、つり合っているとみなすことができます。力（−ma） は見かけの力（慣性力）であり、真の力ではありません。
このように、見かけの力を仮定することで、運動の問題を力のつり合いの問題に帰着させることができるようになります（1743年フランスの数学者ジャン・ル・ロン・ダランベール発表）。
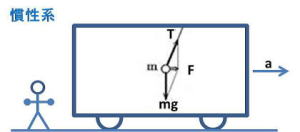
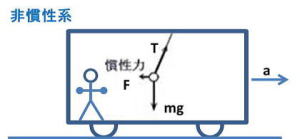図1.慣性系図2.非慣性系
当事務所では人間行動に起因する事故・品質トラブルの未然防止をお手伝いします。また、ものづくりの現場の皆様の声を真摯に受け止め、ものづくりの現場における労働安全の構築と品質の作り込みをサポートします。 （2019.5.26)